今天助教說來畫點特別的＿＿

於是要來畫多光源遠場繞射圖囉！

要多多呢？

不如就5個吧？！

不過這次輕鬆點，就不畫動畫了。

一樣是利用先前的公式和程式，修改如下：

import numpy as np
import matplotlib.pyplot as plt


#定義球面波
def spherical_wave(A, k, r, r0, w, t): #A震幅 k波頻 r向量 r0波源的空間座標 w角頻率 t時間
    dr = np.sqrt(np.dot(r-r0, r-r0)) #r跟r0之間的向量差，得出仍為向量。
    #向量和向量做內積平方後取平方根得出絕對值
    if dr == 0:
        return 1000  #防止除以0 
    phase = complex(0, k*dr-w*t) #k*dr為純量
    #exponential使用負數complex 0為實部，後者為虛部
    return A*np.exp(phase)/dr

#定義lamda為綠光
lamda = 532*10**-9

#定義波三維方向波頻
k = 2*np.pi/lamda

#定義繪圖範圍
D = 0.005

#繪圖細緻度
N =151

#定義空間座標的2維陣列
x_list = [-D/2 +D*i/N for i in range(N)]
y_list = [-D/2 +D*j/N for j in range(N)]

#np.meshgrid產生網格 製作平面
x_2d, y_2d = np.meshgrid(x_list, y_list)


A = 1 #定義震幅
w = 2*np.pi #定義角頻率

#定義光波為2維的矩陣
L_field = np.zeros((N, N), dtype = complex)

#定義畫圖區域
fig, ax = plt.subplots()

#定義光源
S = 5 #5個光源

#定義光源分佈半徑
R = 0.01

#傳播距離Z
Z =  2

#定義不同多光的波源
for source in range(S):
    r0 = np.array([R*np.cos(source*2*np.pi/S), R*np.sin(source*2*np.pi/S), 0]) #R半徑 光源分佈在不同角度
    for i in range(N):
        for j in range(N):
            r = np.array([x_2d[i,j], y_2d[i,j], Z])
            L_field[i, j] += spherical_wave(A, k, r, r0, w, 0)
            #定義光波，+將各波源帶入運算後加入光波中，波源r0，不畫動畫t以0帶入
            
#取光波的實部
L_real = L_field.real

#畫圖使用contour (not plot因為plot只能有兩筆資料，三筆資料兩個變數以上就必須用contourf)    
ax.contourf(x_2d, y_2d, L_real, cmap = "Greens_r", levels = 99) #cmap為等高線圖色階 levels等高線數
plt.show()

畫出來的圖如下：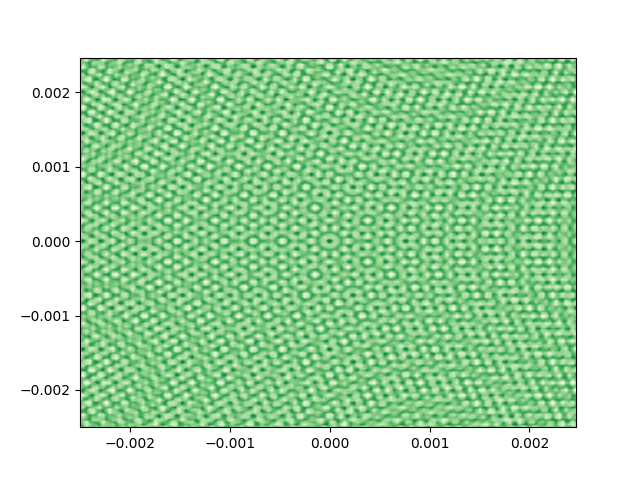

這次修改內容為：

1. 新增光源綠光，以離中心R為半徑均勻分布的5個光源。
2. 增加光源迴圈source，並以矩陣cos,sin的方式定義出source列。
3. L_field[i, j] 後增加 ＋號，讓每個光源算出來都再加入L_field中

大家可以利用這個程式碼玩玩看！
調整光源數S，傳播距離Z，Ｄ繪圖範圍，嘗試畫出不同光源數和距離下，各種美美的繞射圖唷。